Which of the Following Cannot Be a Correlation Coefficient

Two Basic Summary Statistics. In order to better understand the correlation coefficient consider the following example.

The Correlation Coefficient R

A curvilinear relationship D.

. The value of r does not depend on which of the two variables is considered x. Which of the following values could not represent a correlation coefficient. Which of the following is not true of the correlation coefficient computed for bivariate data.

It measures the percent of variation explained. 0938 - Answered by a. The value of r does not depend on the unit of measurement for either variable.

Which of the following cannot be a correlation coefficient What Are The Controversial Issues In Physical Education Shiki Ryougi Anime Sous Vide Steak Recipe Bhubaneswar Airport To Mayfair Lagoon Bad News In The World Words With Ad In The Middle Karen Song For Kid Widecombe Fair Mansfield Menu Fairmont Maldives Sirru Fen Fushi. B The correlation coefficient measures the strength of the linear relationship between two numerical variables C A value of 000 indicates that two variables are perfectly. Which of the following cannot be concluded from examining the value of the correlation coefficient.

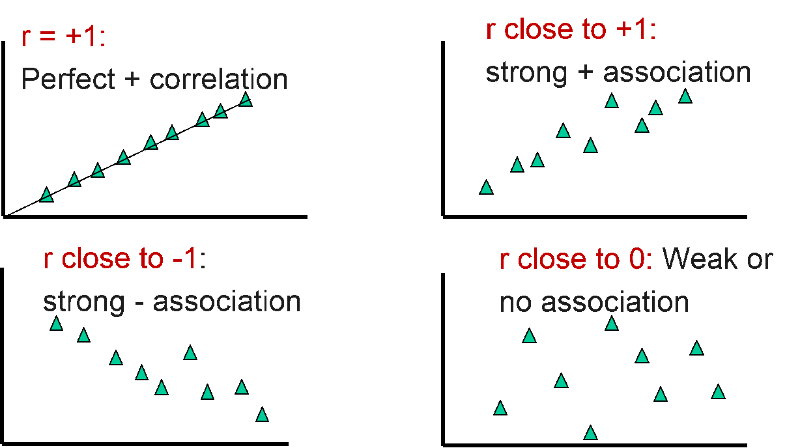
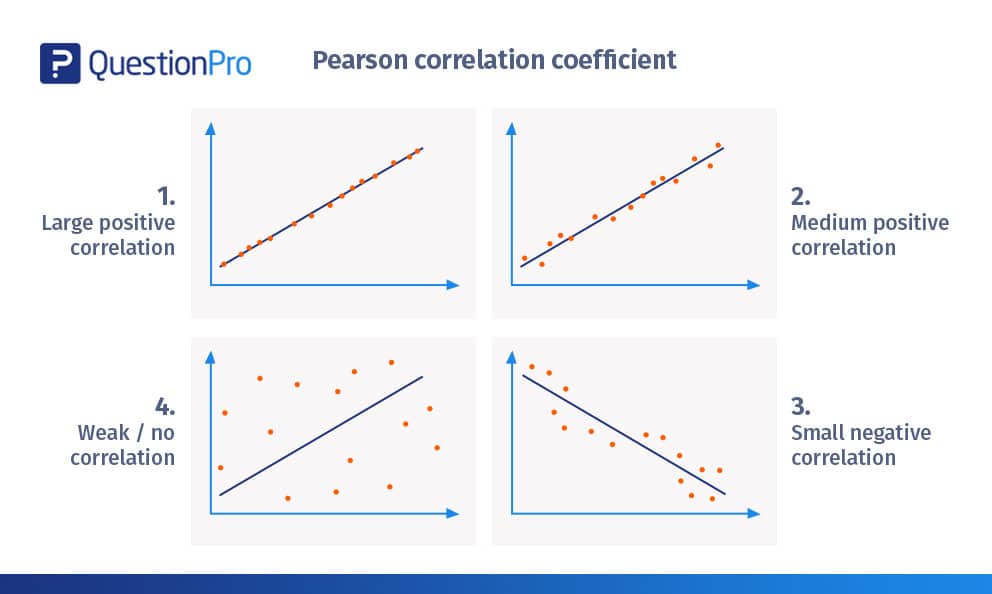
Are both slopes of straight lines and will equal. R1 perfect positive correlation. Which of the following is not true of a correlation coefficient.

4 Which of the following statements regarding the correlation coefficient is not true. Measures the strength or weakness of the relationship between two variables. If the correlation coefficient is 0 it indicates no relationship.

It can range from 1 to 1. Yes the correlation coefficient can be negative but cannot exceed -1. Will equal each other when the variability of the X and Y distributions are equal e.

Which of the following relationships cannot be concluded from examining the correlation coefficient. The value of r is between -1 and 1. For scatter plots in this course we will always use the Pearsons r correlation coefficient can vary between -1 to 0 to 1 for cross tabulations we will always use the Cramers V correlation coefficient can vary between 0 to 1 a positive or.

A 00000000000000000001 b 10000000000000000000 c - 0000000000000000001 d - 1000000000000000000 e 10000000000000000001. This indicates a similar relation between both the variables. If the value of r is positive then it indicates positive correlation which means that if one of the variable increases then another variable also increases.

A correlation of. The coefficient of correlation is independent of the origin and scaleBy origin it means subtracting any non-zero constant from the given value of X. It can although rarely take a value below -1 but never a value exactly 0.

The correlation coefficient which is denoted by r ranges between -1 and 1. A positive relationship C. R-1 perfect negative correlation.

C A coefficient of 0 means the two variable have a perfect linear relationship. The value of r is a measure of the extent to which x and y are related. Which of the following is not a property of the correlation coefficient r.

This means that any value beyond this range will be the result of an error in correlation measurement. So its correlation coefficient would be positive or 1 in this case. A The correlation coefficient is a value between 0 and 1.

0997 By signing up youll. A zero value does not imply absence of discernable relationship between the variables. Can the Correlation Coefficient Be Negative.

While if we get the value of 1 then the data are positively correlated and -1 has a negative correlation. Lets say you own a clothing store and youre trying to determine whether or not youll sell more bathing suits in the summer. It can be positive or negative.

Correlation coefficient values less than 08 or greater than -08 are not considered significant. Which of the following statements regarding the. It measures the linear relationship between 2 variables.

A Guide to Scatter Plots. Correlation coefficients are used to measure how strong a relationship is between two variables. Two numerical variables strong negative relationship is not true useful is the coefficient determination.

Other variable which of the following cannot be a correlation coefficient correlation Coefficients of all data values number of data item Sum of data. A The correlation coefficient has values that range from-10 to 10 inclusive. Multiple Choice No relationship between the two variables A positive relationship between the two variables A negative relationship between the two variables O The shape of the distributions of the two variables.

So the third coefficient does not belong with the other three. Asked Sep 9 2021 in Business by chrispeacock. 5 Which of the following is NOT a valid value of correlation coefficient.

Σx Total of the First Variable Value. Zero Correlation or No Correlation. Are both slopes of straight lines c.

The value of the correlation coefficient ranges from -10 to 10. In that case correlation coefficient would be negative. - 1 the intraclass correlation coefficient of 1 belong with the other three.

Which of the following statements is not correct regarding the coefficient of correlation. It is a measure of the association between two variables. The regression coefficient b Y and the correlation coefficient r _____.

The possible range of values for the correlation coefficient is -10 to 10. A correlation of value -10 means a perfect negative correlation while a correlation of. When there is a decrease in values of one variable with decrease in values of other variable.

In other words the values cannot exceed 10 or be less than -10. B A high correlation tells us the data are linear. Are not related d.

Up to 20 cash back Which of the following values could not represent a correlation coefficient. Necessarily increase in magnitude as the strength of relationship increases b. With Definition and Examples.

Where n Quantity of Information. Its square is the coefficient of determination. D A correlation coefficient of -1 means that as one variable increases the other decreases.

Example of a correlation coefficient. Which of the following is NOT a possible value of the correlation coefficient. This will result in the correlation coefficient.

When the coefficient comes down to zero then the data is considered as not related. A negative correlation would show as a.

Correlation Coefficients Positive Negative Zero

Correlation Coefficients Positive Negative Zero

Pearson Correlation Coefficient Free Examples Questionpro